Steady-state torsional vibration in the crankshaft of an internal combustion engine
Calculation of the steady-state torsional vibration in the crankshaft of an internal combustion engine. Torque produced by each cylinder is calculated from the force produced by the pressure from ignition which is scaled according to the rotation speed of the crankshaft. Torsional vibration analysis based on the article “Analysis of torsional vibration in internal combustion engines: Modelling and experimental validation” [1]. The model is based on Fig.4 of the original article.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import scipy
import opentorsion
from opentorsion import Shaft, Disk, Assembly
[2]:
def pressure_curve():
'''Load digitized pressure curve from csv and pass it to interpolator'''
curve = np.genfromtxt('ICE_example_data/pressure_data.csv', delimiter=';')
return scipy.interpolate.interp1d(curve[:, 0], curve[:, 1])
[3]:
def peak_pressures():
'''Load digitized peak pressure from csv and pass it to interpolator'''
curve = np.genfromtxt('ICE_example_data/peak_data.csv', delimiter=';')
return scipy.interpolate.interp1d(curve[:, 0], curve[:, 1])
[4]:
def scaled_cylinder_pressure(rpm, num_points):
'''
Scales the cylinder pressure curve based on the variation
of peak pressure with engine speed.
Arguments
---------
rpm: float
Rotating speed of the engine in rpm
num_points: int
Number of points in x-axis
Returns
-------
angles: np.ndarray
Angles for which the cylinder pressures are given
scaled_curve: np.ndarray
The scaled pressure curve scaled to the given rpm corresponding
to the angles. (Pa)
'''
# Load the base pressure curve
angles = np.linspace(0, 720, num_points)
base_curve = pressure_curve()
base_curve_sampled = base_curve(angles)/15.2
# Scale with the peak pressure
pressures = peak_pressures()
scaling = pressures(rpm)
scaled_curve = base_curve_sampled*scaling*1e6
return angles, scaled_curve
[5]:
def calculate_cylinder_torque(speed_rpm, num_points=500):
'''
Calculates the torque produced by a single cylinder at given rpm.
Torque is based on the tangential force caused by the pressure in the cylinder and the tangential component
of the oscillating inertial force from the crankshaft spinning.
Parameters
----------
speed_rpm: float
Current rotation speed in rpm
num_points: float, optional
Number of points for the x-axis
Returns
-------
M_t: ndarray
The torque produced by the cylinder
alpha: ndarray
Angles for which the cylinder torques are given
'''
def alpha_to_beta(alpha, r, l_rod):
return np.arcsin(r/l_rod * np.sin(alpha))
l_rod = 0.207 # m
d_piston = 0.105 # m
r = 0.137 / 2 # m (piston stroke / 2) crankshaft radius
m_a = 2.521 # kg
alpha_deg, p_curve = scaled_cylinder_pressure(speed_rpm, num_points)
alpha = alpha_deg/180*np.pi
w = speed_rpm/60*2*np.pi
F_g = p_curve * 0.25*np.pi*d_piston**2
beta = alpha_to_beta(alpha, r, l_rod)
F_tg = F_g * np.sin(alpha + beta) * 1/np.cos(beta) # Tangential gas load
lambda_rl = r/l_rod
F_ia = -m_a*r*(np.cos(alpha)
+ lambda_rl*np.cos(2*alpha)
- lambda_rl**3*1/4 * np.cos(4*alpha)
+ 9*lambda_rl**5*np.cos(6*alpha)/128)*w**2 # Oscillating inertial force
F_ta = F_ia * np.sin(alpha + beta) * 1/np.cos(beta) # Tangential inertial force
F_t = F_tg + F_ta # Total tangential force
M_t = F_t * r
return M_t, alpha
[6]:
def calculate_dft_components(signal, t, num_harmonics):
'''
Calculates dft components and harmonics (0,0.5,1,...) for the given signal, to be used at stedy-state
vibration calculations.
Parameters
----------
signal: ndarray
Cylinder torque
t: ndarray
Crankshaft rotation angle
num_harmonics: float
Number of harmonics considered
Returns
-------
complex ndarray
The first num_harmonics complex components of the Fourier transform
complex ndarray
The first num_harmonics components of the harmonics
'''
dft = np.fft.rfft(signal)/len(signal)
dft[1:] *= 2
omegas = np.fft.rfftfreq(len(signal))*1/(t[1]-t[0])*2*np.pi
return [dft[:num_harmonics], omegas[:num_harmonics]]
[7]:
def crankshaft_assembly():
'''
A shaft-line Finite Element Model of a crankshaft based on model presented
in https://doi.org/10.1243/14644193JMBD126 Fig.4.
Returns
-------
assembly: openTorsion Assembly class instance
The created opentorsion assembly
'''
J2 = 0.0170
J3 = 0.0090
J4 = 0.0467
J5 = 0.0327
J6 = 0.0467
J7 = 0.0467
J8 = 0.0327
J9 = 0.0487
J10 = 2.0750
k2 = 1.106e6
k3 = 1.631e6
k4 = 1.253e6
k5 = 1.253e6
k6 = 1.678e6
k7 = 1.253e6
k8 = 1.253e6
k9 = 1.976e6
c_a = 2 # absolute damping
shafts, disks = [], []
disks.append(Disk(0, J2))
shafts.append(Shaft(0, 1, None, None, k=k2, I=0))
disks.append(Disk(1, J3))
shafts.append(Shaft(1, 2, None, None, k=k3, I=0))
disks.append(Disk(2, J4, c=c_a)) # cylinder 1
shafts.append(Shaft(2, 3, None, None, k=k4, I=0))
disks.append(Disk(3, J5, c=c_a))
shafts.append(Shaft(3, 4, None, None, k=k5, I=0))
disks.append(Disk(4, J6, c=c_a))
shafts.append(Shaft(4, 5, None, None, k=k6, I=0))
disks.append(Disk(5, J7, c=c_a))
shafts.append(Shaft(5, 6, None, None, k=k7, I=0))
disks.append(Disk(6, J8, c=c_a))
shafts.append(Shaft(6, 7, None, None, k=k8, I=0))
disks.append(Disk(7, J9, c=c_a)) #cylinder 6
shafts.append(Shaft(7, 8, None, None, k=k9, I=0))
disks.append(Disk(8, J10)) # flywheel
assembly = Assembly(shafts, disk_elements=disks)
return assembly
[8]:
def relative_damping_C(assembly, d, w):
'''
Updates the damping matrix C of assembly when using frequency dependent relative damping.
Parameters
----------
assembly: openTorsion Assembly class instance
The assembly of whose damping matrix is to be updated
d: float
Loss factor property, used to calculate relative damping
w: float
Angular frequency of the system, used to calculate relative damping
Returns
-------
C: ndarray
The damping matrix assembled with new component specific damping coefficients
'''
if w!=0:
c_r = d/w
else:
c_r = 0
C = np.zeros((assembly.check_dof(), assembly.check_dof()))
if assembly.shaft_elements is not None:
for element in assembly.shaft_elements:
dof = np.array([element.nl, element.nr])
C[np.ix_(dof, dof)] += c_r*element.K()
if assembly.disk_elements is not None:
for element in assembly.disk_elements:
C[element.node, element.node] += element.C()
if assembly.gear_elements is not None:
for element in assembly.gear_elements:
C[element.node, element.node] += element.C()
# Build transformation matrix
E = assembly.E()
transform = assembly.T(E)
# Calculate transformed mass matrix
C = np.dot(np.dot(transform.T, C), transform)
return C
[9]:
def calculate_response(crankshaft, rpm):
'''
Calculates the crankshaft's response to excitation at given rpm.
Parameters
----------
crankshaft: openTorsion Assembly class instance
Opentorsion Assembly of the crankshaft
rpm: float
Current rotation speed in rpm
Returns
-------
sum_response: ndarray
Array containing maximum vibratory torque at current rotation speed for each shaft
'''
dof = 9
cylinder_torque, alpha = calculate_cylinder_torque(rpm)
dft_parameters, harmonics = calculate_dft_components(cylinder_torque, alpha, 25)
q = np.zeros([dof, len(harmonics)], dtype='complex128')
M = crankshaft.M
K = crankshaft.K
d = 0.035
for i in range(len(harmonics)):
# build T vector
offset = 2 # offset to the first cylinder
phase_shift = 2/3*np.pi
T = np.zeros(dof, dtype='complex128')
T[offset] = dft_parameters[i]
T[offset+1] = dft_parameters[i]*np.exp( 2.0j*phase_shift*harmonics[i])
T[offset+2] = dft_parameters[i]*np.exp(-2.0j*phase_shift*harmonics[i])
T[offset+3] = dft_parameters[i]*np.exp( 1.0j*phase_shift*harmonics[i])
T[offset+4] = dft_parameters[i]*np.exp(-1.0j*phase_shift*harmonics[i])
T[offset+5] = dft_parameters[i]*np.exp( 3.0j*phase_shift*harmonics[i])
w = harmonics[i]*rpm*2*np.pi/60
C = relative_damping_C(crankshaft, d, w)
receptance = np.linalg.inv(-w**2*M+1.0j*w*C+K)
q.T[i] = receptance @ T
# Calculate the angle difference between two consecutive disks
q_difference = (q.T[:, 1:] - q.T[:, :-1]).T
shaft_list = crankshaft.shaft_elements
shaft_ks = np.array([shaft.k for shaft in shaft_list])
# Multiply the angle difference between two disks with the connecting shaft stiffness to get
# the torque in the shaft
q_response = (shaft_ks*q_difference.T).T
for i in range(dof-1):
shaft_i = q_response[i]
sum_wave = np.zeros_like(alpha)
for i in range(len(shaft_i)):
this_wave = np.real(shaft_i[i]*np.exp(1.0j*harmonics[i]*alpha))
sum_wave += this_wave
sum_response = np.sum(np.abs(q_response), axis=1)
return sum_response
[10]:
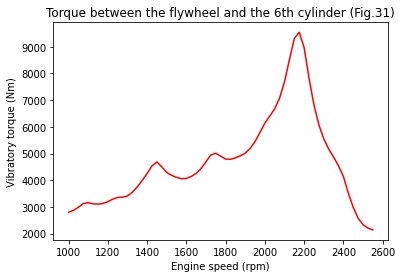
def plot_results(rpms, vibratory_torque):
'''
Plots the vibratory torque in wanted shafts for each considered engine speed.
Parameters
----------
rpms: ndarray
All considered engine speeds in rpm
vibratory_torque: ndarray
Matrix containing maximum vibratory torque at each rotation speed for each shaft.
Each row correspond to an engine speed and each column to a shaft.
Returns
-------
shaft_8: ndarray
Array containing maximum vibratory torque at all considered engine speeds for shaft
between flywheel and 6th cylinder
shaft_1: ndarray
Array containing maximum vibratory torque at all considered engine speeds for shaft
between crankshaft pulley and gear train
'''
shaft_8 = [shaft[7] for shaft in vibratory_torque]
plt.plot(rpms, shaft_8, c='red', label='calculated')
plt.xlabel('Engine speed (rpm)')
plt.ylabel('Vibratory torque (Nm)')
plt.title('Torque between the flywheel and the 6th cylinder (Fig.31)')
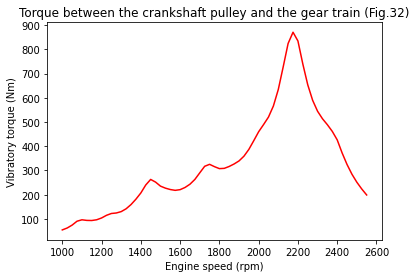
plt.figure()
shaft_1 = [shaft[0] for shaft in vibratory_torque]
plt.plot(rpms, shaft_1, c='red', label='calculated')
plt.xlabel('Engine speed (rpm)')
plt.ylabel('Vibratory torque (Nm)')
plt.title('Torque between the crankshaft pulley and the gear train (Fig.32)')
plt.figure()
return shaft_8, shaft_1
[11]:
assembly = crankshaft_assembly()
rpms = np.arange(1000, 2575, 25)
# Vibratory torque for every shaft and every considered engine speed
vibratory_torque = []
for rpm in rpms:
vibratory_torque.append(calculate_response(assembly, rpm))
shaft_8, shaft_1 = plot_results(rpms, vibratory_torque)
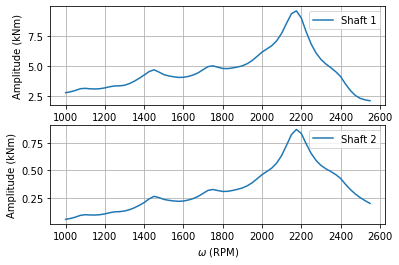
# Same plots but using openTorsions Plots class
plots = opentorsion.Plots(assembly)
plots.torque_response_plot(rpms, [np.array(shaft_8), np.array(shaft_1)], True)
[1] Mendes AS, Meirelles PS, Zampieri DE. Analysis of torsional vibration in internal combustion engines: Modelling and experimental validation. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics. 2008;222(2):155-178. doi:10.1243/14644193JMBD126